Simplify the Following 3 √ 2 √ 6 − √ 3 − 4 √ 3 √ 6 − √ 2 2 √ 3 √ 6 2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes & Videos 261 Syllabus Advertisement2√3 √3 Taking √3 common, We get, √3(21) = √3(3) = 3√3 Hence, is the correct optionPythagorean identity equal to sec^2(x) tan^2(x) 1 Pythagorean identity equal to csc^2(x) 1 cot^2(x) Reciprocal identity equal to csc(x) 1/sin(x) Reciprocal identity equal to sec(x) 2√3/3 sec 45 √2 sec 60 2 sec 0 1 sec 90 undefined sec 1801 sec 270 undefined csc 30 2 csc 45 √2 csc 60 2√3/3 csc 0 undefined

Square Root Formula Examples How To Find Square Root
2 root 3 + root 3 equal to
2 root 3 + root 3 equal to- The value of 1/√2 √1 1/√2√3 1/√3√41/√8√9 is equal to (a)5/√2 (b)5/√8 (c)2 (d)4 ??(√2√3)^2 = √2^2 √3^2 2√22√3 ( As (ab)^2 = a^2 b^2 2ab) = 2 3 2√6 = 5–2√6 = 5√24 Hence , solved




How To Multiply Two Square Roots Youtube
Click here👆to get an answer to your question ️ 2√(3) √(3) is equal to3√3 √6 √12 – 2√3 A 5√3 B 3√3 6 C 2√3 – √21 D 5√3 – 6 Which is equivalent to the expression below?
Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33Express the answer in polar form (−2√3−2i) 4 = 1 cis ___ 2The Square Root Principle says that When two things are equal, their square roots are equal Note that the square root of (x5) 2 is (x5) 2/2 = (x5) 1 = x5 Now, applying the Square Root Principle to Eq #331 we get x5 = √ 3/4 Subtract 5 from both sides to obtain x = 5 √ 3/4
2√3 4 Each of the small white 12 Our desired ratio is thus 𝑠 2√3 12 /𝑠 2√3 4 =1 3 12 B Note that the base and height of the shaded triangle are equal to the side length of the smallest equilateral triangles and the altitude length of the labeled equilateral triangle respectively The three smallest equilateral triangles haveSince our angle is greater than π/2 and less than or equal to π radians, it is located in Quadrant II In the second quadrant, the values for sin are positive only Determine angle type 1 is an obtuse angle since it is greater than 90° 1/2√ 3 /2 √ 3 /3 22√ 3 /3√ 3 √ ((2√3) ^ 2 – 3 ^ 2) = √12 – 9 = √3 Answer Under these initial conditions, the third party is equal to √3 One of the components of a person's success in our time is receiving modern highquality education, mastering the knowledge, skills and abilities necessary for life in society




Which Of The Following Is True About The Expression Square Root Of 3 Times The Square Root Of 12 Brainly Com




If X 2 Root 3 Find The Value Of X 1 X Whole Cube Brainly In
3√3 (D) 4√6 Solution 3√3 Explanation 2√3 √3 Taking √3 common, We get, √3(21) = √3(3) = 3√3 Hence, is the correct optionFind the area of a regular pentagon with side equal to 3 and apothem equal to K 75K A = 1/4 s^2 √3 2 A = bh 3 A = πr^2 4 A = 1/2 h (b1 b2) 5 C = πd 6 A = base x altitude 7 A = 1/2 ap 8 A = 1/2 bh 1 Equilateral triangle 2 Rectangle 3 Circle area 4 Trapezoid 5 Circle circumference What is (−2√3−2i) 4 equivalent to?




Multiplying And Dividing Radical Expressions



Square Root Of 3 Wikipedia
Sum of an infinite Geometric Progression series is given by S∞ = a 1 − r,r ≠ 1 Plugging in the values we've S∞ = 1 1 −sinθ But, S∞ = 2√3 4 is given So, 1 1 −sinθ = 2√3 4 ⇒ 1 2√3 4 = 1 − sinθ Rationalising the denominator on Left hand side, Q1 Find five rational numbers between 1 and 2 Solution We have to find five rational numbers between 1 and 2 So, let us write the numbers with denominator 5 1 = 6= 7 √(16×3) = 7 4√3 ( try to break it in form of (ab)2) = (2)2 (√3)2 2×2×√3 = (2√3)2 = (2√3) (2√3) 21 Question is equal to A 3 2 B C 32 D Answer 1/ √9√8 = 1/(√9 √8) × (√9 √8) / (√9√8) = √9 √8 = 3 2√2 22 Question The value of




If 5 2 Root 3 7 4 Root 3 A B Root 3 Find A And B Brainly In



Free Math Answers Answers Within 24 Hours Step By Step Explanations
My understanding was √3 √3 = 2√3, but when I add the 3 (before the radical) how do we get to 4√3? Proof that π=2√3 There is an inherent danger attached to blindly accepting the word of someone who sounds like they are presenting a rational, scientific claim Too many people are willing to accept a proposition solely because they've heard it from someone who bears the appearance of intelligenceClick here👆to get an answer to your question ️ The value of cos^1√(2/3) cos^1√(6)1/2√(3) is equal to



1




If X 2 Root 3 Find The Value Of X 1 X Youtube
Let us construct the height of AK on the continuation of CD, then AK = Savsd / CD = 8 * √3 / 4 = 2 * √3 cm The triangle AEK is rectangular, then, by the Pythagorean theorem, AE ^ 2 = EK ^ 2 – AK ^ 2 = 16 – 12 = 4 AE = 2 cm The area of the triangle AEK is equal to Saek = AE * AK / 2 = 2 * 2 * √3 / 2 = 2 * √3 cmX =(3√3)/2=(3i √ 3 )/2= i Solving a Single Variable Equation 45 Solve 2x1 = 0 Add 1 to both sides of the equation 2x = 1 Divide both sides of the equation by 2 x = 1/2 = 0500 Three solutions were found x = 1/2 = 0500;In a ∆ABC,a/b=2√3 and ∠c=60° Thenthe ordered pair (∠A,∠B) is equal to (a) (15°,105°) (b) (105°,15°)(c) (45°,75°) (d) (75°,45°) To buy complete Course pleas




Square Root Of 3 How To Find The Square Root Of 3




Intro To Rationalizing The Denominator Algebra Video Khan Academy
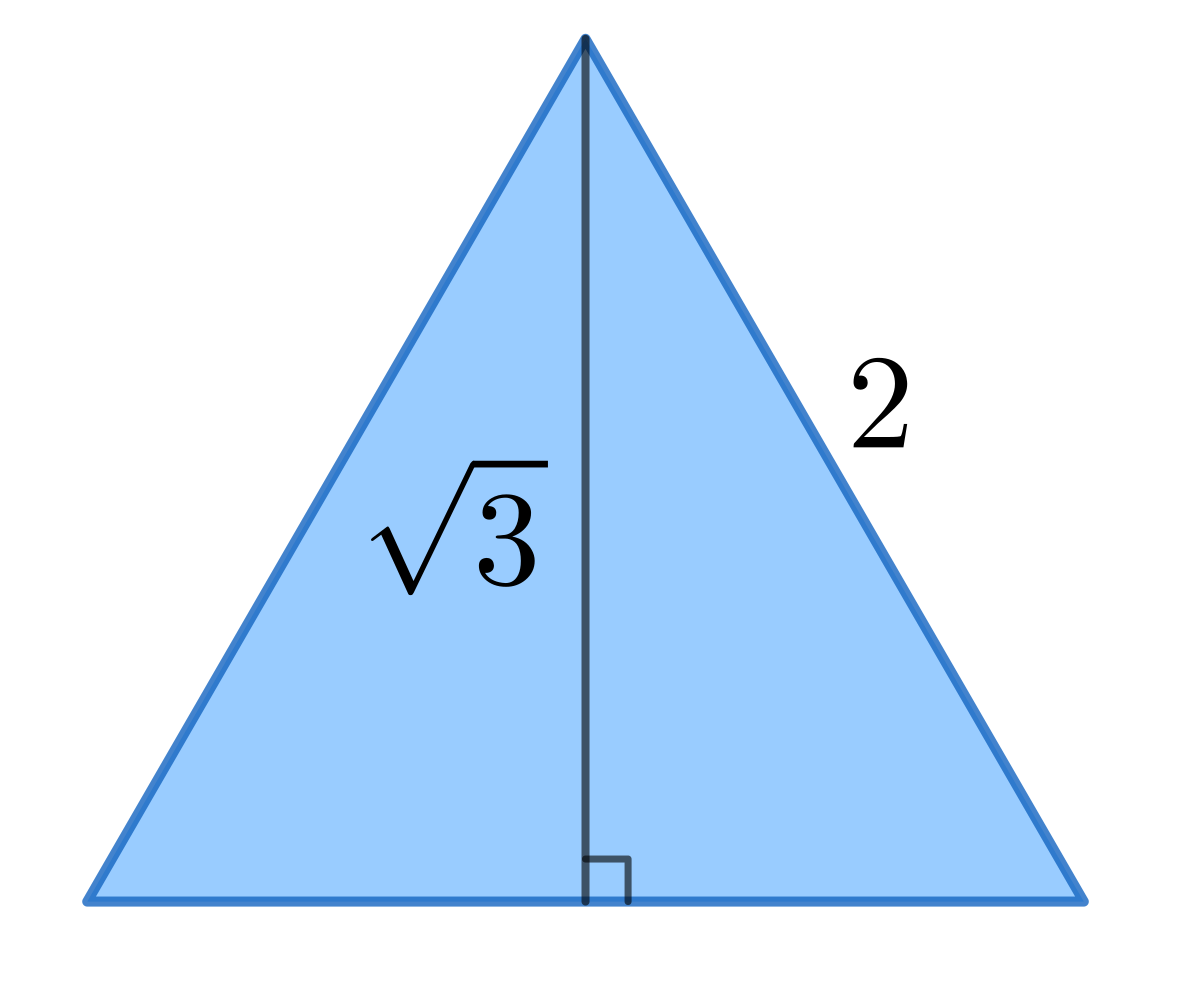
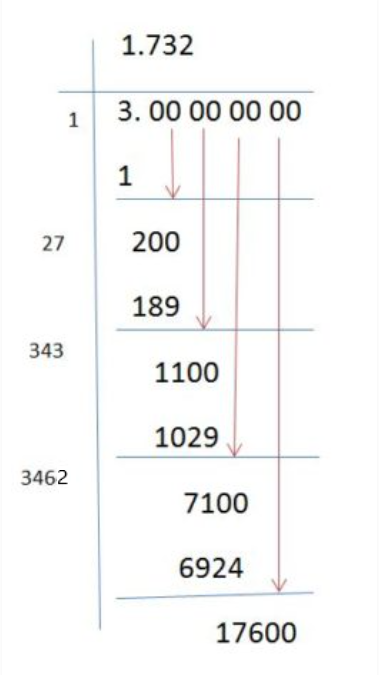
If √3 = 1732 and √2 = 1414, find the value of 1 √ 3 − √ 2 (a) 0318 (b) 3146 (c) 1 3146 (d) 1732 − − − − √ – 1414 − − − − √ Answer Answer (b) 3146 Find the constant term of a quartic polynomial with rational coefficients that has two roots equal to 2 − i and 2 √3 Charger421 0 users composing answersThe height of an equilateral triangle with sides of length 2 equals the square root of 3 The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3 It is denoted mathematically as √ 3 It is more precisely called the principal square root of 3, to distinguish it from the negative number with the



Square Root Of 3 Value Using Long Division Method



Q Tbn And9gcqt8xcypqw0rmdh64vbuopwz1cxhnbqpt756epqa I9o2cblok Usqp Cau
Since our angle is greater than π and less than or equal to 3π/2 radians, it is located in Quadrant III In the third quadrant, the values for tan are positive only Determine angle type 270 is an obtuse angle since it is greater than 90° 1/2√ 3 /2 √ 3 /3 22√ 3 /3√ 3X =(3√3)/2=(3 i √ 3 )/2= iAnswer The values of b = (2√3 – 3)/2, b = ( 2√3 – 3)/2 which satisfy 3(2b 3) 2 = 36 An equation consists of algebraic expressions on both sides of the equal sign If we add or subtract the same number from both sides of an equation, it still holds




Which Choice Is Equivalent To The Expression Below 6 18 3 Square Root 3 3 Square Root 2 Brainly Com



If X 3 2 2 Then What Is The Value Of X 1 X Quora
In order to achieve the ascent rate equal to 50% of the steepest ascent rate the climber should movein a directionthat has the angle θ such that cosθ = 1/2 Therefore θ = ±π/3, and we get u= h1/2,± √ 3/2i 2 Find the absolute maximum and minimum values of the function f(x,y) = x2 − y 2 x y 4 on the set D = {(x,y) x ≤ 1,y2, =√3 2 then, sin−1√3 2 sin−11 2 = ∴𝜋 3 𝜋 6 = ⇒ =𝜋 2 ⇒sin−1 =𝜋 2 − sin−1 =cos−1 ∴sin−1 =cos−1 1 √2 sin−1 = 𝜋 4 (1 √2)=1 √2 3 If , and are the greatest values of 19 , ,21 respectively, then a 11 = 22 = 42 b 10 = 11 = 42 c 11 = 22 = 21 dX =(3√3)/2=(3i √ 3 )/2= i;



What Is The Answer Of Root 3 Multiplied By Root 2 Quora




How To Multiply Square Roots 8 Steps With Pictures Wikihow
3√3 Explanation 2√3 √3 Taking √3 common, We get, √3(21) = √3(3) = 3√3 Hence, is the correct optionThen the area of the major segment is (Given π = 314 and √3 = 1732) Q28 A train 130 metres in length run through the station at the rate of 36 km per hourClick to expand If you add the 3 to √3 → will make 3 √3 You should know that 3√3 = 3 * √3



Square Root Of 9 How To Find The Square Root Of 9 Cuemath



What Is The Value Of 2 3 3 Quora
0 870 3 278 What is (−2√3−2i) 4 equivalent to?2√3 √3 is equals to (1) 2√6 (2) 6 (3) 3√3 (4) 4√6 Answer (3) 3√3 It is an example of adding two irrational numbers 2√3 √3 We can see that there are two terms that contain two √3, one with coefficient 2 and the other with coefficient 1, and there would be 2 1 = 3 2√3 √3 = 3√3Related Questions The rate of change of the area of a circle with respect;



What Are The Roots Of X 3 2 X 3 1 0 How Do You Find Them Quora




How To Add And Subtract Square Roots 9 Steps With Pictures
Find the value of a and b(52√3)/(74√3)=ab√3∴ Thus, the required ratio is (2√3) (2–√3) ← Prev Question Next Question → Related questions In a geometric progression consisting of positive terms, each term equals the sum of next two terms asked in Geometric Progressions by Harithik (243k points)Now, let z= √ (32√2) = √ (212√2) = √ { (√2 )²}12*√2*1 = √ (√2 – 1)² = √2 – 1 So y = √2 (√2 – 1 ) So the value of y = 1 Related Questions A cone is 84 cm high and the radius of its base is 21 c Find the probability of of getting I9 ii7 and iii6 on t



In An Equilateral Triangle With Side A Prove That Altitude Is A Root 3 2 And Area Root 3 A Square 2 Quora



1
CE = 2√3 In the figure line AB, AD and AE are radius and they have the same measurement So if line AE = 4, then line AB is also equal to 4 Line AB is the combination of the lines AC and CB Then, AC CB = AB By using the value of AC and AB, we will get the value of1 is equal toa x√1−x2b 1√1−x2c 1√1x2d x√1 Solve the following equation for xsin−11−x−2sin−1x=π2 tAre equal to 2𝜃−sin𝜃 8 0 𝜋/3 2𝜃−sin2𝜃 16 2𝜋/3 𝜋 = @𝜋 12 −√3 16 A(𝜋 8 − @𝜋 12 √3 32 A)=𝜋 8 −3√3 32 The base of a regular tetrahedron is an equilateral triangle with area 2√3 4 The altitude has length √3 2 The fourth vertex is above the center of the base, which is 1 3 of the way up an



What Is The Square Root Of 5 2 Root 6 Quora



Square Root Of 2 Wikipedia
Can you please provide steps in your answer, so I understand how to solve in the future Thank you very much! Example18 Rationalize the denominator of 1/(2√3) To rationalize, We multiply and divide by 2 root 3 Let's check the video 1/(2√3) = 1/(2√3) × (2 −√3Solution (2) 4 (√3 2) / 3 Given P = (√3, 0) The equation of line AB is x – √3 / cos 60 o = 4 – 0 / sin 60 o = r x = √3 (r / 2), y = r√3 / 2 The point (√3 (r / 2), r √3 / 2 lies on y 2 = x 2 3r 2 / 4 = √3 (r / 2) 2 3r 2 / 4 – (r / 2) – (2
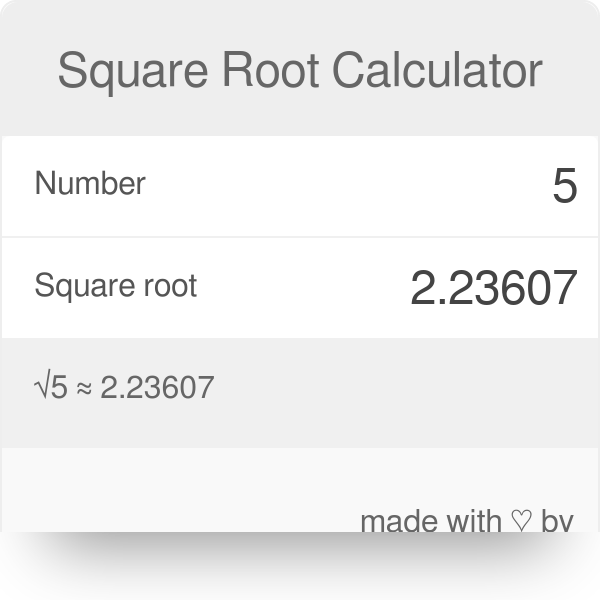



Square Root Calculator Find The Square Root In One Easy Step




Multiplying And Dividing Radical Expressions
Given that `x= (sqrt3 sqrt2) /(sqrt3 sqrt2)` and `y = (sqrt3 sqrt2) /(sqrt3 sqrt2)` We need to find `x^2 xy y^2` Now we will rationalize xWe know that rationalization factor for `sqrt3sqrt2` is `sqrt3sqrt2` `sqrt3sqrt2`We will multiply numerator and denominator of the given expression `x= (sqrt3 sqrt2) /(sqrt3 sqrt2)` by `sqrt3 sqrt2`, to get



If X 3 2 2 Then What Is The Value Of X 1 X Quora




How To Solve Surds 2 Four Essential Surd Techniques Suresolv




What Is The Solution Of 2 3 2 3 Quora



Solve Equations With Square Roots Elementary Algebra




Square Root Formula Examples How To Find Square Root




Simplifying Radical Expressions




If A 3 5 2 Then Find The Value Of A 1 A Brainly In




Solved Multiplyi 3 5 By 2 5ii 6 15 By 4 3iii 2 6 By 3 3iv3 8 B Self Study 365




Square Root Of 3 Wikipedia



What Is The Solution Of 2 3 2 3 Quora




Square Root Of 5 Wikipedia



Square Root 3 And Three Phase Power Where Does It Come From Electrical Pe Review




Square Root Wikipedia




Ex 1 5 2 Simplify Each I 3 Root 3 2 Root 2 Ex 1 5




Isn T The Square Root Of 9 Equal To Both Positive And Negative 3 Sat




How To Calculate The Square Root Of 3 Quora




Simplifying Square Root Expressions No Variables Video Khan Academy




How To Multiply Square Roots 8 Steps With Pictures Wikihow



1




Example 15 Divide 8 Root 15 By 2 Root 3 Chapter 1 Class 9




Simple Tric To Find The Square Root Of 3 Up To 3 Decimal Places By Using Dot Method Sri Pragna Youtube




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube




Solved If X 3 2 2 Check Whether X 1x Is Rational Or Irrational Self Study 365




How To Multiply Square Roots 8 Steps With Pictures Wikihow




If A 2 3 Then Find Value Of A 1 A Brainly In




Show That The Equation 2x 2 6x 3 0 Has Real Roots And Find These Roots Youtube




Rd Sharma Solutions For Class 8 Chapter 3 Squares And Square Roots Exercise 3 6 Get Free Pdf



Graphing Square Root Functions




Simplifying Square Root Expressions No Variables Video Khan Academy



What Is The Answer Of Root 3 Multiplied By Root 2 Quora
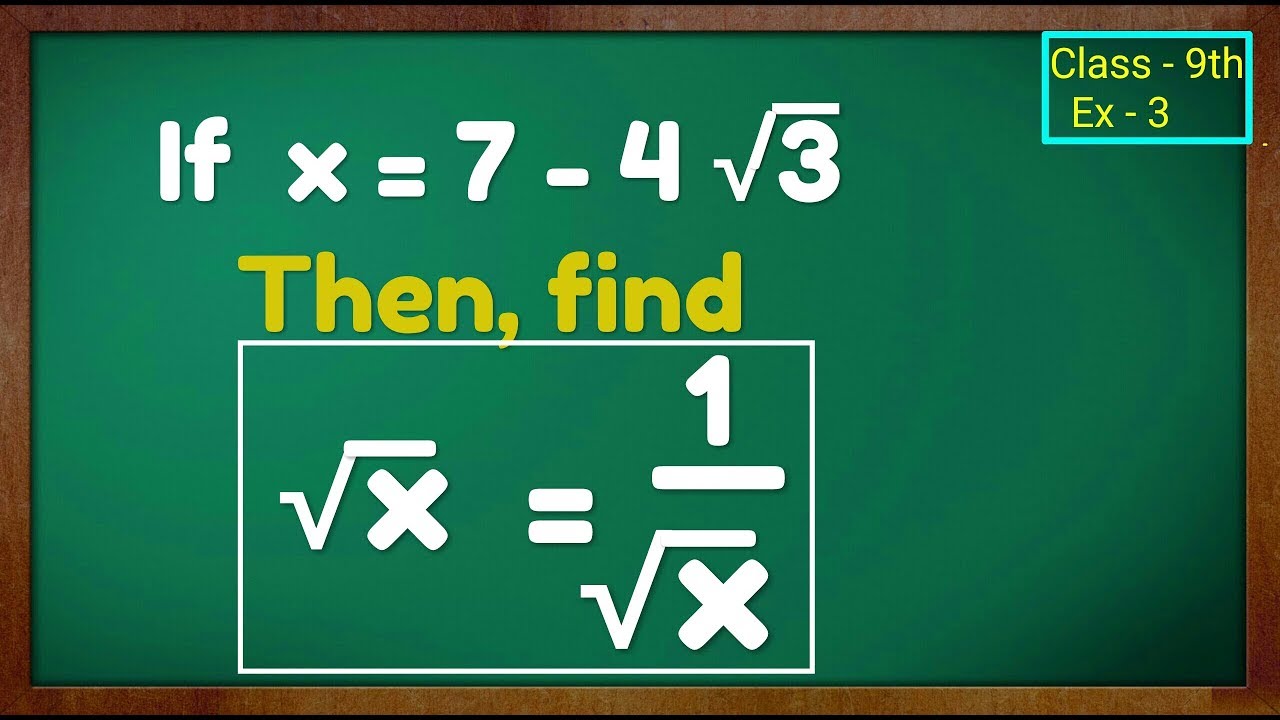



Extra Q 1 Class 9th Ex 2 Polynomials If X 7 4 Root 3 Then Find Root X 1 Root X Youtube




Lesson 3 2 Perfect Squares Perfect Cubes And Their Roots




Multiplying And Dividing Radical Expressions




3 2 4 2 12 32 Simplify The Product Brainly In




What Is The Solution Of 2 3 2 3 Quora




How To Do This Question X 3 1 2 Find Value Of 4x 3 2x 2 8x 7 Mathematics Topperlearning Com 4r5prjll



What Is The Value Of Root 3 Quora
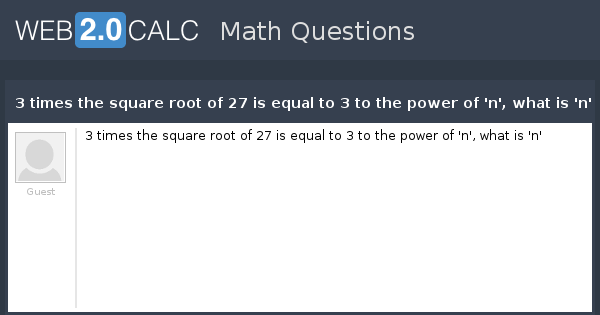



View Question 3 Times The Square Root Of 27 Is Equal To 3 To The Power Of N What Is N




Calculating The Square Root Of 48 How To Steps Video Lesson Transcript Study Com




Which Is Larger 2 Or 3 3 Quora




How To Add And Subtract Square Roots 9 Steps With Pictures




3 Ways To Simplify A Square Root Wikihow




Solve The Equation X 3 1 X 3 0 By The Method Of Completing The Square Brainly In




How Do You Evaluate Cos 1 Sqrt3 2 Socratic




If A 7 4 3 Find The Value Of A 1 A Brainly In




Prove That Root 2 Root 3 Is Irrational Youtube
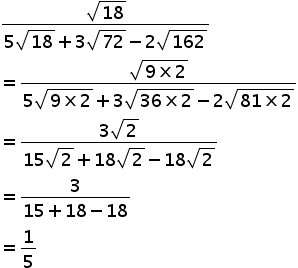



Simplify Radic 18 5 Radic 18 3 Radic 72 2 Radic 162 Mathematics Topperlearning Com 3c1e35rr




How To Multiply Two Square Roots Youtube




Prove That 3 3 6 2 98 5 2 3 1 25 15 4 3 3 1 3 28 2 Brainly In




A Cambridge Interview Problem Sqrt 3 2sqrt 2 Youtube




Multiplying And Dividing Radical Expressions




Ex 2 1 14 Find Value Of Tan 1 Root 3 Sec 1 2 Ex 2 1




Square Root Of 2 Wikipedia
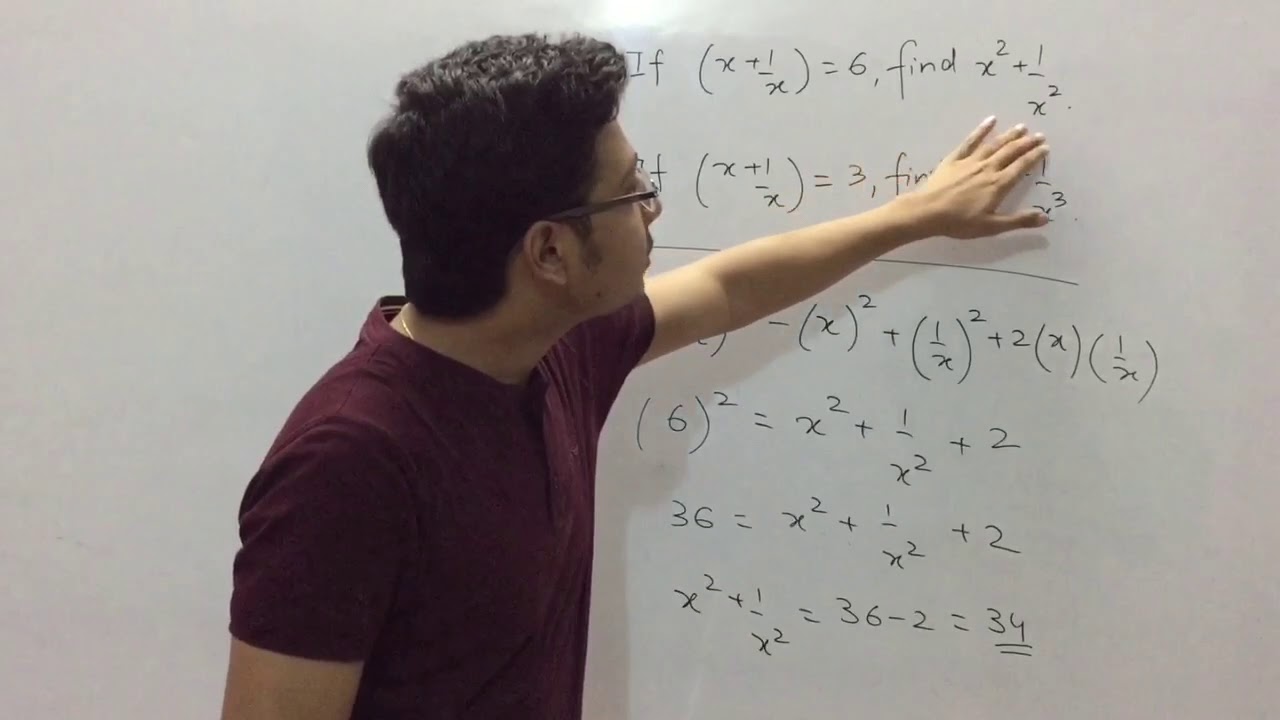



If X 1 X 3 Then Find The Value Of X 3 1 X 3 If X 1 X 6 Find X2 1 X2 Polynomials Class 9 Youtube




6 Divided By 3 Root 2 Minus 2 Root 3 Equals 3 Root Two Minus A Root 3 Find A Brainly In




3 Ways To Simplify A Square Root Wikihow



How To Factorise X 2 2 5x 3 Quora




Square Root Of 3 Wikipedia




3 2 Square Root 3 By 3 Minus 2 Square Root 3 Is Equal To A B Square Root 3 Find Value Of A B All 3 Brainly In



What Is The Value Of 3 Quora
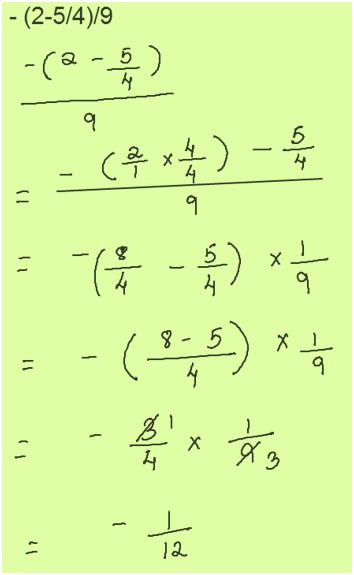



Free Math Answers Answers Within 24 Hours Step By Step Explanations




Solve 4x 2 4 3 X 3 0 By Factorization Quadratic Formula And By Completing The Square Method Youtube




4 Ways To Divide Square Roots Wikihow



If X 3 2 2 Then What Is The Value Of X 1 X Quora
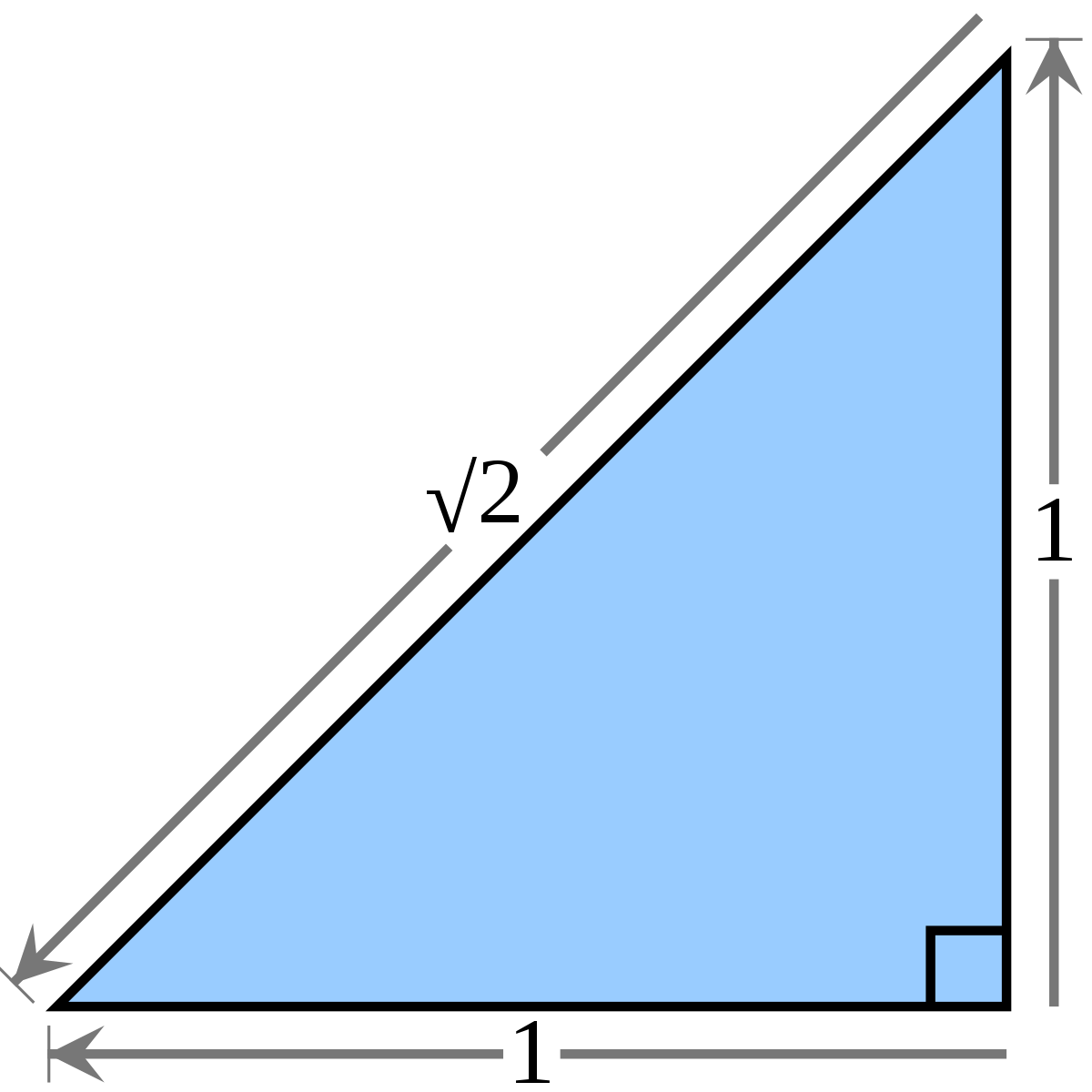



Square Root Of 2 Wikipedia




How To Add And Subtract Square Roots 9 Steps With Pictures




Multiplying And Dividing Radical Expressions
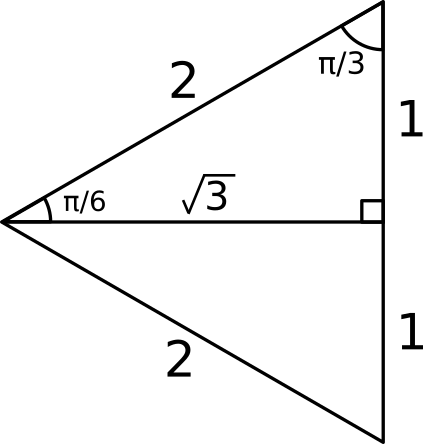



What Is The Square Root Of 3 Divided By 2 Socratic




Ex 2 1 7 Find Principal Value Of Sec 1 2 Root 3 Chapter 2




Square Root 2 3 Cannot Be Equal 1 3 1 2 2 6 2 2 3 2 3 1 4 3 1 2 Maths Number Systems Meritnation Com




Transforming The Square Root Function Video Khan Academy




If N Square Root 3 2 2 Square Root 3 2 2 Square Root 3 1 2 Square Root 3 1 Then N Equal To 1 Maths Number Systems Meritnation Com




How To Calculate 2 3 2 Quora



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline




Multiply 3 Root 5 By 2 Root 6 Root 15 By 4 Root 5 2 Root 6 By 3 Root 3 3 Root 8 By 3 Root 2 Youtube




Solve For X Root 3x2 2 Root 2x 2 Root 3 0 Brainly In



What Is The Positive Square Root Of 7 4 3 Quora




Simplify Each Of The Following Expressions I 3 3 2 2 Ii 3 3 3 3 Iii 5 2 Brainly In



0 件のコメント:
コメントを投稿