Answer a Explanation √23 = Since the decimal expansion of the number is nonterminating nonrecurring Hence, it is an irrational number MCQ PART2 Question 1 The value of 22−−√3− −−−√4 is equal to (a) 2–16 (b) 26 NCERT Solutions Class 9 Maths Chapter 1 Exercise 15 Question 2 Summary Thus, the simplified values of (3 √3) (2 √2), (3 √3) (3 √3), (√5 √2)², and (√5 √2) (√5 √2) are 6 3√2 2√3 √6, 6, 7 2√10 and 3 respectively3 A triangle PQR, which is right at P such that ZQ = 22PRQ And perimeter of APQR is 7√3(√31)cm then what is its area?

Evaluvate Cos Cos Inverse Square Root 3 2 Pi 6 Maths Inverse Trigonometric Functions Meritnation Com
3 2 2 answer
3 2 2 answer-That means if we have any hope of a nice denesting of a b 2 then N ( a b 2) needs to be a perfect square We check 3 2 − 2 2 ( 2) = 1 is indeed a perfect square This will give the principal value if the radicand is real Let's apply it to our problem; Click here 👆 to get an answer to your question ️ Given that 2√2−√5 / 3√22√5 = = jesutemisola jesutemisola Mathematics Middle School answered Given that 2√2−√5 / 3√22√5 = = 1 See answer what are p and q on your equation?




3 Ways To Simplify A Square Root Wikihow
C ( √3 — 9 ) 2 d ( 4√5 — 10 ) e ( √15 ) 3 f ( √3 — 27 ) 4 Writing Expressions in Radical Form Work with a partner Use the properties of exponents and the defi nition of a rational exponent to write each expression as a radical raised to an exponent Then use a calculator to evaluate each expression Round your answer to twoFind the angle between two vectors a = {3; The square root of \(1\) is \(i\) and the square root of \(4\) is \(2\) We get 2i*i*2√3 We simplify that and get 4√3 2 Which expression is equal to 2√−28?
⚡ Ответы ⚡ на вопрос Сократите дробь 3√3 √15√5 2√2 √6√3 otvet5com The nth term of a sequence is 3 2 Work out the first three terms of the sequence 3 What is the coefficient of range for the following distribution?Answer (1 of 9) The problem, (√2√3)^2 =(√2)^2(√3)^22(√2*√3) =232√6 =52√6 Now, 2√6=√24=(approx) So, (√2√3)^2 =52√6 =54
Answer The Euclidean distance between points A (3, 2) and B (4, 1) is √2 units Example 2 Prove that points A (0, 4), B (6, 2), and C (9, 1) are collinear Solution To prove the given three points to be collinear, it is sufficient to prove that the sum of the distances between two pairs of points is equal to the distance between the thirdFormula(√x 1/√x)^2 = x 1/x 2 or, (√x1/√x)^2 = (3–2√2) 1/(3–2√2) 2= 5–2√2 1×(32√2)/(3–2√2)×(32√2) Find the zeroes of the polynomial 2s^2 (1 2√2)s 2, and verify the relation between the coefficients and the zeroes of the polynomial asked in Polynomials by Sima02 ( 494k points)



If A 3 2 3 2 And B 3 2 3 2 Then How Do I Find A 2 B 2 Quora




Is There A Solution For X For X 2 Y Sqrt 3 X 2 2 1 Mathematics Stack Exchange
Find the value of √(30√30√30∞) A) 4 B) 6 C) 5 D) 33 Chapter 1 c2 1 2 ( √ 3 ) 2 4 ⇒ c √ 4 2 d2 1 2 2 2 5 ⇒ d √ 5 e2 1 2 (√ 5 ) 2 6 ⇒ e √ 6 f 2 1 2 ( √ 6 ) 2 7 ⇒ f √ 7 g2 1 2 ( √ 7 ) 2 8 ⇒ g √ 8 2 √ 2 The length of "c" is a rational number 13 Since the length of the carpet equals the sum of the height49√3 cm² (A) 27(√31)



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Simplifying Square Root Expressions No Variables Video Khan Academy
√ 2) Therefore Q(√ 2) with the usual operations is a subfield of R (b) By contradiction assume that √ 3 ∈ Q(√ 2), ie there exist a,b ∈ Qsuch that √ 3 = a b √ 2 Then (ab √ 2)2 = (a22b2)2ab √ 2, so one gets 3−a2−2b2 = 2ab √ 2 Since √ 2 ∈ Q the only possibility is that 2ab = 0, which implies that either aUNIVERSIDAD AUTÓNOMA DEL CARMEN CAMPUS I FACULTAD DE CIENCIAS QUÍMICAS Y PETROLERAS INGENIERÍA QUÍMICA TRABAJO SOLUCIONARIO MATEMÁTICAS I ALUMNA BAUTISTA NOLASCO VIVIANA GUADALUPE FECHA fLibro Stanley Grossman Ejercicios 31 En los problemas del 1 al12 encuentre la magnitud y dirección del vector dado 1V = ( 4,4 ) θ Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33



Solved X 3 Square Root 1 3 Square Root 2 What Is X X Is A Binomial With A Mixed Radical And Constant Course Hero



Solved Find The Equation Of Tangent Line To F X 3 Square Root X 3 3 Sq Root X 2 2 At X 1 Put Answer In Standard Form Slope Of The Tangent Lin Course Hero
2 X∞ n=1 cos2(n) √ n3 Solution Since 0 ≤ cos2(n) √ n3 ≤ 1 n3 2, and X∞ n=0 1 n3 2 converges by pseries test (p = 3 2 >1), then comparison test yields the convergence of X∞ n=1 cos2(n) √ n3 b 6 points Decide whether each of the following series converges absolutely, converges conditionally or diverges Circle your answerThere are several ways to go about it Finding The Actual Value Method Here we find the actual value of x, which is nothing but 3 2* (), which is approximately equal to Now we can evaluate the expression (√x1/√x), by taking negative square root for both the parts (√x) and (1/√x)2} Solution calculate dot product of vectors a b = 3 4 4 4 0 2 = 12 16 0 = 28 Calculate vectors magnitude a = √ 3 2 4 2 0 2 = √ 9 16 = √ 25 = 5 b = √ 4 2 4 2 2 2 = √ 16 16 4 = √ 36 = 6 Calculate the angle between vectors



1




Surds Objectives Grade A Rationalise The Denominator Of A Surd Such As Grade A Simplify Surds Such As Write In The Form Ppt Download
Radical and root calculator Result, where index is equal to 6 Formula is 6 √ x 6 √05 009 ルート(√)の足し算、引き算、掛け算、割り算は、中学3年生で習う数学です。 足し算、引き算、掛け算、割り算の計算は以下のようになります。 足し算:√2+√2=2√2 引き算:2√2ー√2=√2 掛け算:√2×√2=2 割り算:2√2÷√2=2 とにかく覚えてしまえば良い? それ1019 29 3039 4049 5059 Class Interval Frequency (a) 22 11 25 16 7




Ex 1 5 2 I Simplify 3 3 2 2 Class 9 With Video




Expert Verified Simplify Each Of The Following Expressions I 3 3 2 2 Ii 3 3 3 3 Iii Brainly In
Because √3 is being added to itself 2 times, we can plug it into this formula, giving us this number 2(√3), or 2√3 We can also approximate the answer Because √3 is irrational, it would go on forever, so, if we want to give a rational answer, we need to approximate itRationalise the denominator of 1/√3√2 and hence evaluate by taking √2 = 1414 and √3 = 1732,up to three places of decimal asked in Class IX Maths by muskan15 Expert (380k points) real numbers 1 voteIi 2(−√2√6√10)≈371 iii 2(−6√3√5√7)≈123 i ii iii, 2 The following table shows speedometer readings at 10second intervals during a one minute period during the race for a car racing at the Daytona International Speedway in Florida t(s) 0 10 30




Solved Multiplyi 3 5 By 2 5ii 6 15 By 4 3iii 2 6 By 3 3iv3 8 B Self Study 365




Square Root 3 Square Root 2 Mathematics Topperlearning Com 5h9ymjj
So if we average them to get a new starting point x ′, the new pair ( x ′, 2 / x ′) will be closer to √2 than the first one 1 Start with any positive number x 2 Calculate 2 / x 3 Take the average of x and 2 / x 4 Repeat steps 2 and 3 until satisfiedRationalise the denominator of 1/√3√2 and hence evaluate by taking √2 = 1414 and √3 = 1732,up to three places of decimal asked in Class IX Maths by muskan15 Expert (For example, the multiplication 3√5∙2√10 might lead a student to the product 6√50 However, this product can be simplified A student might start simplifying the square root of 50 by creating a factor tree that starts with the factors of 5 and 10




Rd Sharma Solutions Class 9 Maths Chapter 3 Rationalisation Updated For 21 22



What Is The Value Of 3 2 2 Quora
Can be written in the form √2, where , and are integers Find, in terms of , an expression for and an expression for Question 13 Categorisation As above, but involving multiples of surds Edexcel IGCSE May15(R)4H Q19c Edited ( −2√3) 2 = −√3 where and are integersIf They Are AP Find the Common Difference 3, 3 √ 2 , 3 2 √ 2 , 3 3 √ 2 Maharashtra State Board SSC (English Medium) 10th Standard Board Exam Question Papers 238 Textbook Solutions MCQ Online Tests 39 Important Solutions 2786 Question Bank Solutions 9112Rationalise the Denominators of 2√5 3√2/2√5 3√2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 Concept Notes & Videos 431 Syllabus Advertisement Remove all ads Rationalise the Denominators of 2√5 3√2/2√5 3√2 Mathematics




Find A Quadratic Polynomial Whose Zeroes Are 3 2




Multiplying And Dividing Radical Expressions
Sorry about that I have corrected itPlan Use algebraic manipulation to find x Then find the conjugate (x 1/x) by substituting and simplifying Part 1 Find x x 1/x = √5 Multiply both sides of the equation by x x^2 1 = √5x => x^2 √5 x 1 = 0 By subtracting √5 x from both sides of the equation This is the key to eliminating square roots from the denominator Note that (1 − √2 √3) is only a partial conjugate for (1 √2 √3) Multiplying these two expressions will eliminate terms in √2 but leave terms in √3 If we want to rationalise the denominator, we will also need to multiply by some expression of the form a b√3




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download




100以上 32 ニスヌーピー 壁紙
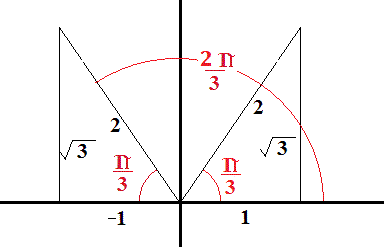
We have a = 3, b = − 2, d = 2, c = 1∴2cos𝜃=−1 and 2sin𝜃=−√3 ⇒cos𝜃=−1 2 and sin𝜃=−√3 2 Since both the values of sin𝜃 and cos𝜃 are negative and sin𝜃 and cos𝜃 are negative in III quadrant, Argument=−(𝜋− 𝜋 3)= −2𝜋 3 Therefore, the modulus and argument of the complex number −1−√3𝑖are 2 and −2𝜋 3 respectively Transcript Simplify (√5√7)^2 (√5√7)^2 =572√35 =𝟏𝟐𝟐√𝟑𝟓 = (√5)^2 (√7)^22√5 √7 About the Author Davneet Singh Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at Teachoo




Expert Answer Find The Value Of A And B If 3 2 3 2 A B 2 Brainly In




Add 3 2 7 3 And 2 5 3 Rational Numbers Video Teachoo
4i√7 −4i√7 4√7i −4√7 Again, we do what we did last time 28=1*4*7 We can move out the 1 and the 4 to get 2*i*2√7 We simplify this and get 4i√7 (note0} and b = {4;√ √23 3 23 = 795ei09 4 Consider De Moivre's Theorem, which states that (cosθ isinθ)n = cosnθ isinnθ This follows from taking the nth power of both sides of Euler's theorem Find the formula for cos4θ and sin4θ in terms of cosθ and sinθ




Working With Square Roots Warm Up 1 3 3 2 4 4 3 5 5 4 1 1 5 3 3 6 5 6 Simplify 7 24 8 18 9 81 10 Ppt Download




Rationalize The Denominator Meaning Methods Examples
勾股 勾股定理说明:在直角三角形里,斜边的平方等于另外两边的平方的和: x 2 y 2 = 1 2 但 1 2 是 1,所以: x 2 y 2 = 1 (单位圆的方程) 因为 x=cos 和 y=sin,我们得到: (cos(θ)) 2 (sin(θ)) 2 = 1 一个有用的 "恒等式" 重要的角:30°、45° 和 60° 你应该尝试牢记这些角度的正弦、余弦和正切的Get an answer for 'Simplify 2√27 5√8 3√18 4√12 and show how to do it, please' and find homework help for other Math questions at eNotesAnswer (1 of 2) √(72√10) = √5√2 and √(62√5) = √51 So LHS is (√5√2)/(√51) = (√5√2)(√5−1)/4 = (√252√5−√5−√2)/4 = √a




3 Ways To Simplify A Square Root Wikihow




Evaluvate Cos Cos Inverse Square Root 3 2 Pi 6 Maths Inverse Trigonometric Functions Meritnation Com
1Simplify the radical expression √56√√5 A5√5 √10 C7√5 D5√10 2Simplify the radical expression 2√63√96 A14√6 B14√96 C5√96 D50√6 3Simplify the radical expression (8√11)(8√11) A53 MATH Find and simplify the difference quotient for the given function f(x)= x^22x1 I need to know how to set up= (√ 3) 2 (√ 2) 2 2 √ 3 √ 2 3 − 2 Using identity, (a b) 2 = a 2 b 2 2 a b = 3 2 2 √ 6 1 = 3 2 2 √ 6 ∴ x = 5 2 √ 6 − ( i ) On squaring both sides, we get, 🔴 Answer 1 🔴 on a question Calculați a b – c pentru a) a = 2√3 – 5, b = 3√2 – 2√3, c = –5 3√2 b) a = 2 – √5 , b = – 4√7 2√5 , c = √5 – 4√7 the answers to answerhelpercom




Add 2 3 5 2 And 3 2 2 2 2 5 3 7 5 And 3 3 2 5 2 3 7 1 2 2 6 11 Youtube



What Is The Square Root Of 5 2 Root 6 Quora
Write whether 2√453√ 2√5 on simplification gives as rational or an irrational number Mathematics Q 5 Simplify (4 5)−5 ×(53 43)−3 Mathematics NCERT Standard VIII Q 1 Simplify (i) 25×t−4 5−3×10×t−8 (ii) 3−5×10−5×125 5−7×6−53 Proof This follows from the squeeze theorem, the estimate 1 ≤ n p n √ n ≤ n √ 2n = n √ 2n √ n, and lim n→∞ n 2 = lim n→∞ n = 1 2213(a) Suppose that {a The product 3√2 4√2 12√32 equals to (a) √2 (b) 2 (c) 12√2 (d) 12√32 individually in the form whose index will be equal to LCM




A Cambridge Interview Problem Sqrt 3 2sqrt 2 Youtube




An 2 If 4 3 5 4 3 5 A B V5 A B Are Rational Numbers Math
∴ √2 is the simplest form of the rationalising factor of √32 Now, 5√2 x √2 = 5 x 2 = 10, which is a rational number ∴ √2 is the simplest form of the rationalising factor of √50 Now, 3√3 x √3 = 3 x 3 = 9, which is a rational number ∴ √ 3√ 2/2 du u = lnu1√ 2/ = ln1−ln √ 2/2 = −ln √ 2/2 §63 18 Let y = e2x/3 Find the derivative of y with respect to x Answer Using the chain rule, dy dx = e2x/3 d dx (2x/3) = 2 3 e2x/3 38 Suppose lnxy = exy Find dy/dx Answer To find this derivative, we must use implicit differentiation If




Square Root Of 3 Wikipedia
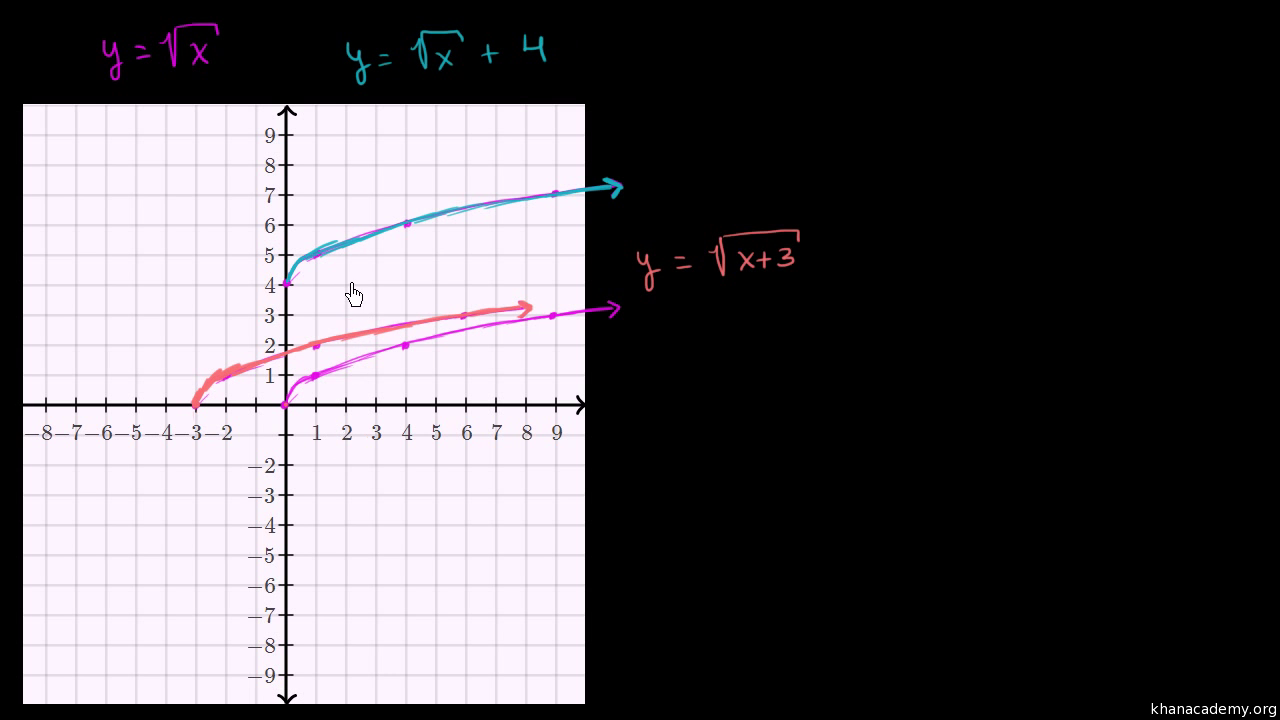



Transforming The Square Root Function Video Khan Academy




Example 4 Graph A Translated Square Root Function Graph Y 2 X 3 2 Then State The Domain And Range Solution Step Graphing Quadratics Function Of Roots




Solved Solve The Equation By The Square Root Property 6x Chegg Com




How To Solve Surds 2 Four Essential Surd Techniques Suresolv




Find The Square Root 1 3 2 4 Ppt Video Online Download



3 Value



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline



If X Square Root 3 2 Then What Is The Value Of The Square Root Of 1 X Plus Square Root 1 X Quora




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V




Graphing X 3 2 Y 3 2 1 Mathematics Stack Exchange
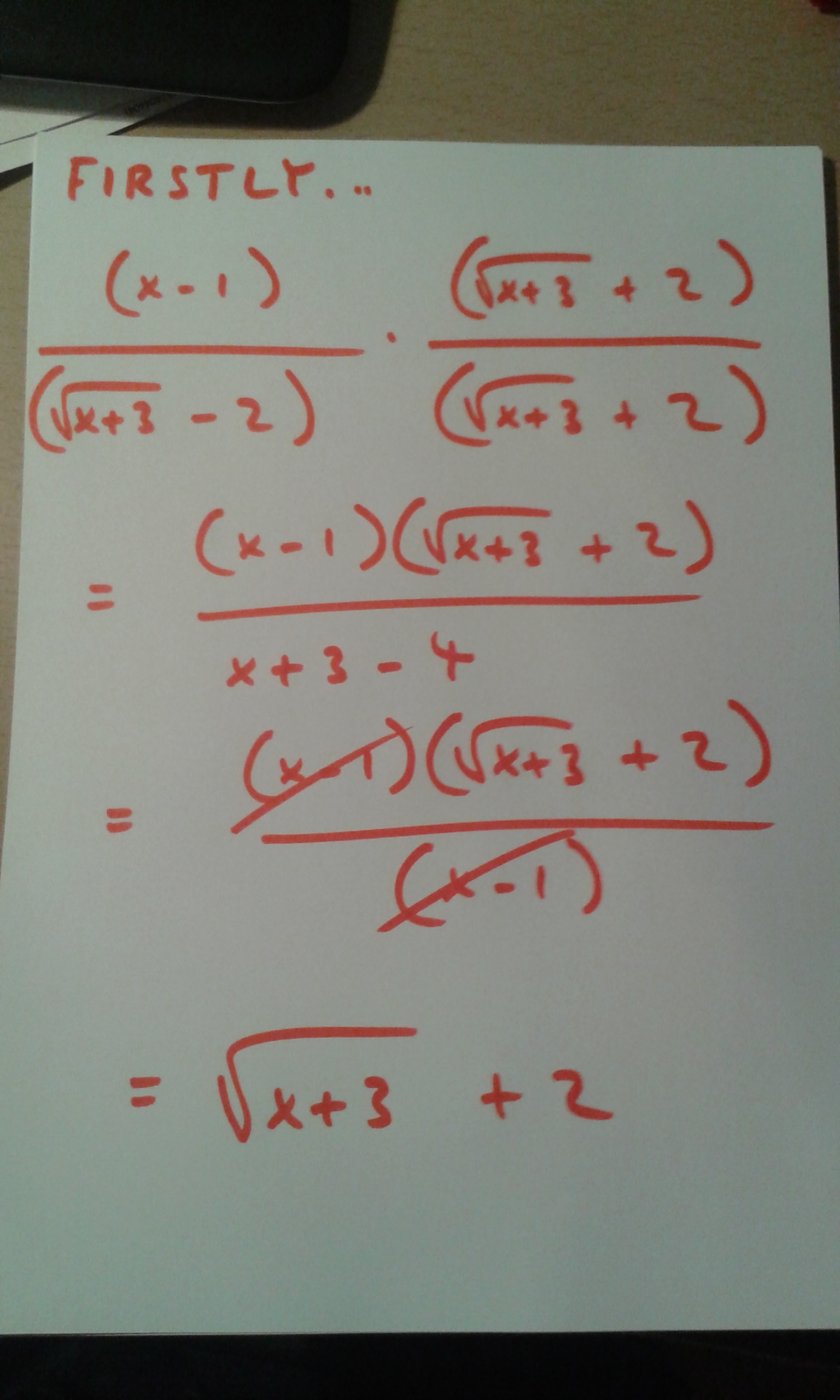



How Do You Find The Limit Of X 1 Sqrt X 3 2 As X Approaches 1 Socratic




3 Ways To Simplify A Square Root Wikihow




Which Of The Following Expressions Are Polynomials In One Variable And Which Are Not State Reasons For Your Answer I 4x 2 3x 7 Ii Y 2 2 Iii 3 T T 2



What Is The Positive Square Root Of 7 4 3 Quora




Cp Alg 2 5 6 Radical Expressions




The Product Root3 2 Root4 2 Root12 32 Equal To A Sqrt 2 B 2 C Root12 2 D Root12 32 Youtube




Solved Cos 2 Theta Square Root 3 2 Cos 2 Theta Chegg Com



How To Calculate 2 3 2 Quora




Solved Find F X 3x 2 4 F X 2 Square Root X 3 2 Chegg Com




2 3 2 3 2 3 2 3 3 1 3 1 Simplify Brainly In




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising




Rationalize The Denominator Of 1 3 2under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66




Square Root 2 3 Cannot Be Equal 1 3 1 2 2 6 2 2 3 2 3 1 4 3 1 2 Maths Number Systems Meritnation Com
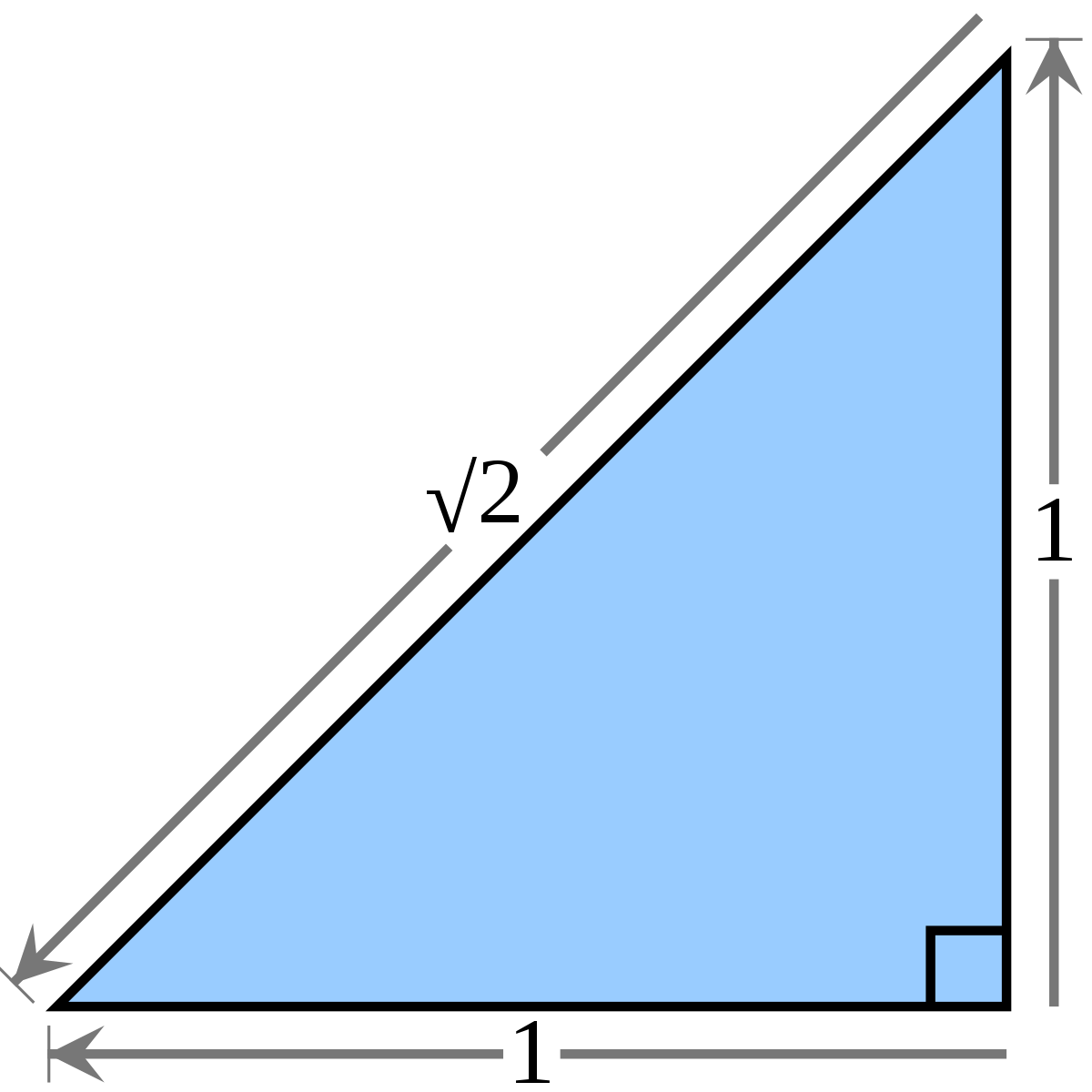



Square Root Of 2 Wikipedia




Solved Square Root 5 Square Root 3 Square Root 15 3 Square Chegg Com



Solution If Cos Of Theta Is Sqrt 3 2 And Theta Is In Quadrant 2 Then Find The Exact Values Of The Other Five Trigonometric Functions I Don 39 T Really Understand How To Do




If X 3 8 Find The Value Of X 2 1x 2




3 Ways To Simplify A Square Root Wikihow




Surds What Is A Surd Manipulating And Simplifying Surds Ppt Download




Prove That 2 3 Is Irrational Given That 3 Is Irrational Video




Extract The Square Root Of A 2 Left Frac Left 3a Sqrt A Right 2 Right Left Frac Left 3 Sqrt A Right 2 Right Frac 41a 16 1 Mathematics Stack Exchange




Solved If X 13 2 3 Find The Value Of X 1x Self Study 365



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community



If X 3 2 2 Then What Is The Value Of X 1 X Quora



Simplifying By Rationalising The Denominator 1 3 2 5 Studyrankersonline




Simplify 2 6 3 54 Youtube
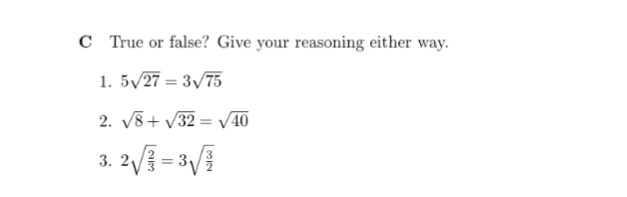



Solved True Or False Give Your Reasoning Either Way 5 Chegg Com



3
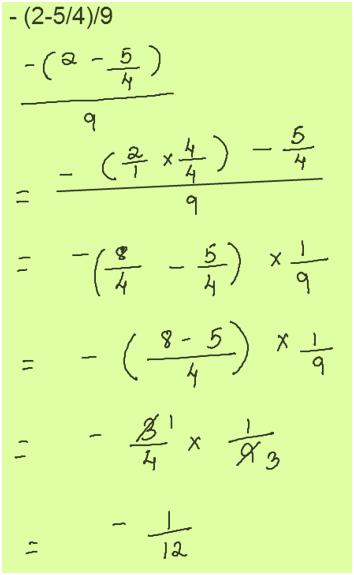



Free Math Answers Answers Within 24 Hours Step By Step Explanations
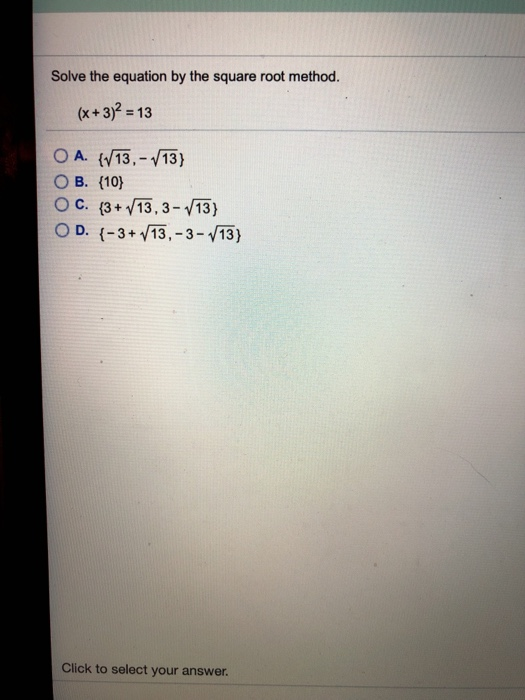



Solved Solve The Equation By The Square Root Method X 3 2 Chegg Com



Graphing Square Root Functions




Multiply 3 2 3 4 3 2 Brainly In




Square Root Of 279 How To Find Square Root Of 279 Solved




Rationalize The Denominator 3 2 5 3 2 Brainly In




How To Add And Subtract Square Roots 9 Steps With Pictures




A Cambridge Interview Problem Sqrt 3 2sqrt 2 Youtube



Express Each One Of The Following With Rational Denominator I 1 3 2 Ii 1 6 5 Iii 16 41 5 Sarthaks Econnect Largest Online Education Community




Find The Square Root Of X 2 9 9 4x 2 X 3 3 2x 5 4




Solved If X 3 2 2 Check Whether X 1x Is Rational Or Irrational Self Study 365



What Is The Solution Of 2 3 2 3 Quora




Rationalize The Denominator 6 3 2 2 3 Brainly In




Solved The Zeros Of The Polynomial 4x2 5 2x 3 Are A 3 2 2 Self Study 365




Multiplying And Dividing Radical Expressions




If N Square Root 3 2 2 Square Root 3 2 2 Square Root 3 1 2 Square Root 3 1 Then N Equal To 1 Maths Number Systems Meritnation Com




Simplify 1 1 2 1 2 3 1 3 4 Brainly In




Solved 3 2 4 2 12 32 Simplify The Product Brainly In



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community
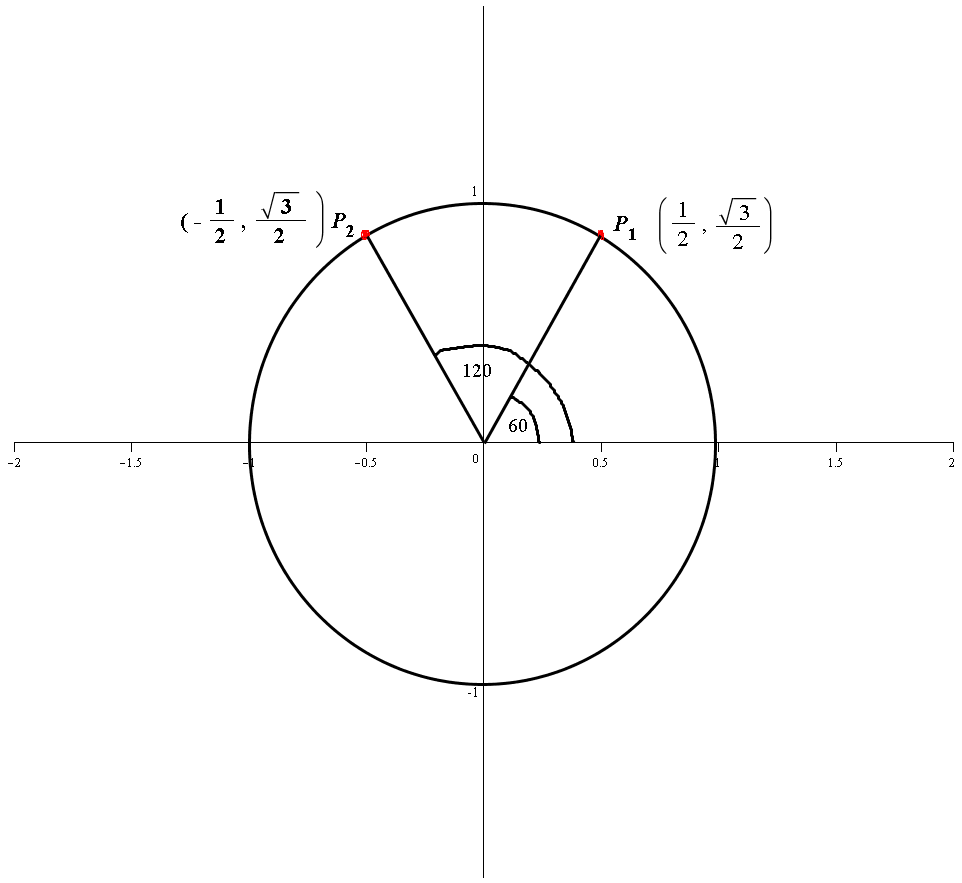



If The Point X Sqrt 3 2 Is On The Unit Circle What Is X Socratic



Solved Sin X Square Root 2 2 X Pi 3 Cos X 1 2 X Chegg Com




Rationalize 2 3 5 2 2 3 3 Brainly In



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora




Transforming The Square Root Function Video Khan Academy



What Is The Sin 1 Sqrt 3 2 Socratic




Example 18 Rationalize The Denominator Of 1 2 Root 3




Find Value Of A And B 3 6 3 2 A B 3 Mathematics Topperlearning Com Lujm5xqq



Simplify 2 Square Root Of 3 5 Square Root Of 2 Gauthmath




Solving Quadratic Equations By Square Root Method By




4 The Square Root Of 3 Sqrt 5 Is A Sqrt 3 2 1 Sq




How To Multiply Square Roots 8 Steps With Pictures Wikihow




Simplifying Radical Expressions




College Algebra Chapter 2 Equations Equations With Square Roots Explanation And Examples Part 3 Alexander Street A Proquest Company




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube



If X 3 2 2 What Is The Value Of X 2 1 X 2 Quora




View Question Simplify 75 2 3 2



1



0 件のコメント:
コメントを投稿